November 2015 ~ Zone Kawruh

Fungsi Riemann Zeta

Fungsi Riemann Zeta, riemann zeta function adalah fungsi bervariabel kompleks $s$ pada setengah bidang $Re(s)>1$ yang didefinisikan sebagai absolute konvergen

$\varsigma(s)=\sum_{n=1}^{\infty}\frac{1}{n^{s}}$

Artinya jika $c=a+bi\in\mathbb{C}$ dengan $a>1$ maka $\varsigma(c)$ konvergen ke suatu titik di kompleks dan $|\varsigma(c)|<\infty$ . Jika dilakukan analytic continuation (perluasan domain), domain $\varsigma(s)$ diperluas menjadi seluruh bidang $\mathbb{C}$ tidak hanya pada $Re(s)>1$ maka fungsi riemann zeta menjadi

$\varsigma(z)=\pi^{z-1}2\sin(\frac{\pi z}{2})\Gamma(1-z)\zeta(1-z)$ (I)

untuk semua $z\in\mathbb{C}$ dan $\Gamma(1-z)$ adalah fungsi gamma yang didefinisikan
$\Gamma(x)=\int_{0}^{\infty}t^{x-a}e^{-t}dt$
untuk $x\in\mathbb{C}$ dan $Re (x)>0$
(note fungsi gamma tidak akan menghasilkan nol, jadi tidak ada $x$ yang memenuhi $\Gamma(x)=0$

Hubungan dengan bilangan prima

Euler menemukan hubungan anatara fungsi riemann zeta dengan bilangan prima yang disebut dengan euler prodak

$\varsigma(s)=\prod_{p}(1-\frac{1}{p^{s}})^{-1}$

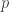Untuk $Re(z)>1$ dan $p$ prima, dari sini bisa kita liat bahwa $\varsigma(s)$ tikan akan mennghasilkan nilai nol jika $Re(s)>0$ dari sini berakibat pada persamaan (I) bahwa $\varsigma(z)$ akan bernilai nol ( $\varsigma(z)=0$ ) jika $z=\{\ldots-4,-2\}$ bilangan genap negatif (hayoo..kenapa bisa begitu) yang disebut dengan trivial zeros

Riemann Hipotesis

Riemann bertanya apaka ada pembuat nol di $\varsigma(s)$ selain trivial zero? Bagaimana dengan titik-titik di $0\leq Re(s)\leq1$ ? adakah titik diantara $0\leq Re(s)\leq1$ yang menyebabkan $\varsigma(s)=0$ ?

Melalui perhitungan yang cukup panjang akhirnya riemann menemukan suatu hipotesis

Pembuat nol pada $\varsigma(s)$ selain trivial zeros mempunyai bagian real bernilai 1/2 dengan kata lain jika ada $x$ yang bukan temasuk trivial zeros dimana $\varsigma(x)=0$ maka $Re(x)=1/2$

Yang namanya hipotesis adalah pernyataannya yang diyakini kebenarannya tetapi belum bisa dibuktikan secara matematis, sampai saat ini belum ada yang mampu membuktikannya, apakah benar atau salah?

Apa istimewanya Hipotesis Riemann

Banyak para matematikawan percaya bahwa hipotesis riemann itu merupakan kunci untuk membuka tabir misteri bilangan prima, selama ini kita tahu bahwa bilangan prima itu tidak berpola muncul secara acak sebarang, jika ada yang mampu membuktikan hipotesis riemann (baik benar maupun salah) kita akan mampu melihat pola dari bilangan prima. Apa yang akan terjadi jika kita bisa melihat pola dari bilangan prima? maka kita dengan mudah melihat pola acak dari peristiwa alam seperti gempa, gunung meletus, tsunami, banyak orang yang percaya bahwa dengan terbukanya tabir misteri bilangan prima maka misteri alam semesta lain pun akan tersingkap, sebelum kita mampu membuat pesawat antar galaxy seperti Voyager pada Film Starterk atau bahkan mesin waktu sekalipun kita harus memacahkan hipotesis riemann,

Suatu yayasan swasta nirlaba Clay Mathematics Institute di Cambridge, Massachusetts, Amerika, telah menawarkan uang senilai US$ 1 juta kepada siapa pun yang dapat memecahkan salah satu dari tujuh permasalahan matematika itu.

Bagaimana anda tertarik memecahkannya?

Note

$Re(x)$ disini adalah bagian real dari bilangan kompleks $x$

Sunday, November 1, 2015

Hipotesis Riemann

Fungsi Riemann Zeta

Hubungan dengan bilangan prima

Riemann Hipotesis

Apa istimewanya Hipotesis Riemann